Table of contents
Open Table of contents
들어가며
카라추바(Karastuba) 알고리즘은 소련의 수학자 아나톨리 알렉세예비치 카라추바가 1960년에 발견하고, 1962년에 공개한, 큰 정수에 대한 효과적인 곱셈 알고리즘
x: B진법의n자리 수 어떤 값y: B진법의n자리 수 어떤 값
기본적으로 x*y의 곱셈연산은 이라는 연산횟수가 필요.
카라추바(Karastuba): 큰 두 수 x와 y의 곱을 자릿수가 x, y의 절반인 수들의 곱, 3번과 덧셈과 시프트 연산을 이용해 연산 횟수를 줄임. -> Time Complexity가 줄어듦.
얼마나 줄어드나요?
- 충분히 큰
n - 작은
n에 대하여는 추가적인 덧셈과 시프트 연산 때문에, 고전적인 곱셈법보다 속도가 느려짐 - 컴퓨터의 환경에 따라 효율성에 차이가 있음
- 일반적으로 곱하는 수가 이상일 때 카라추바 알고리즘이 더 빠르게 처리
예
- 일반적인 방법은 1000자리 숫자를 연산하는 경우 1000의 제곱, 1,000,000의 단자리수 곱셈이 필요
- 카라추바 알고리즘을 이용하면 번의 단자리수 곱셈만 필요
- 일반 곱셈법의 5.9% 만 필요함
알고리즘
의 연산을 위해, 하기와 같이 쪼갬.
-
일반적으로
n자리인 경우m=n/2
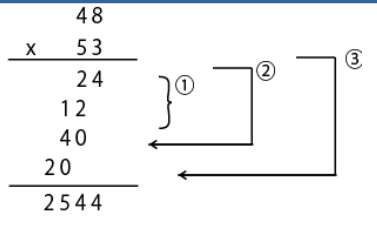
예: 48 * 53
- 일반적인 경우
- 4번의 곱셈
n의 자리의 3번에 덧셈
- 카라추바 알고리즘인 경우
L = 20, N = 20, M = 20 + 24 - (4 - 8)(5 - 3) = 52
xy = 20 * 10^2 + 52 * 10^1 + 24 = 2000 + 520 + 24 = 2544
python 코드
import sys
sys.setrecursionlimit(10**9)
def get_karatsuba(x, y):
if x < 10 or y < 10:
return x * y
n = max(len(str(x)), len(str(y)))
n2 = n // 2
a = x // 10**n2
b = x % 10**n2
c = y // 10**n2
d = y % 10**n2
ac = get_karatsuba(a, c)
bd = get_karatsuba(b, d)
ad_bc = get_karatsuba(a + b, c + d) - ac - bd
result = ac * 10 ** (2 * n2) + ad_bc * 10**n2 + bd
return result
if __name__ == "__main__":
x = 2462
y = 8014
print(get_karatsuba(x, y))
How to Run
python version: 3.11.6
Run main.py
pip install pipenv
pipenv --python 3.11.6
pipenv run python3 main.pyInput
2462와 8014를 곱하는 상황
Output
19730468Execution Image