BOJ 백준 2011: 암호코드

Table of contents

들어가며

걸린 시간: 41분

이 문제를 처음 읽고 든 생각은 다음과 같았습니다.

아 이거 알고리즘 강의 시간에 풀었었는데…

근데 접근 방식과 풀이 방법은 전혀 기억이 나지 않았고 (정말 찜찜하고 기분이 나쁜 상태로), 일단 “가지수”를 세는 것이길래 일단 DP를 의심하면서, 개수를 천천히 세어 나갔습니다.

접근

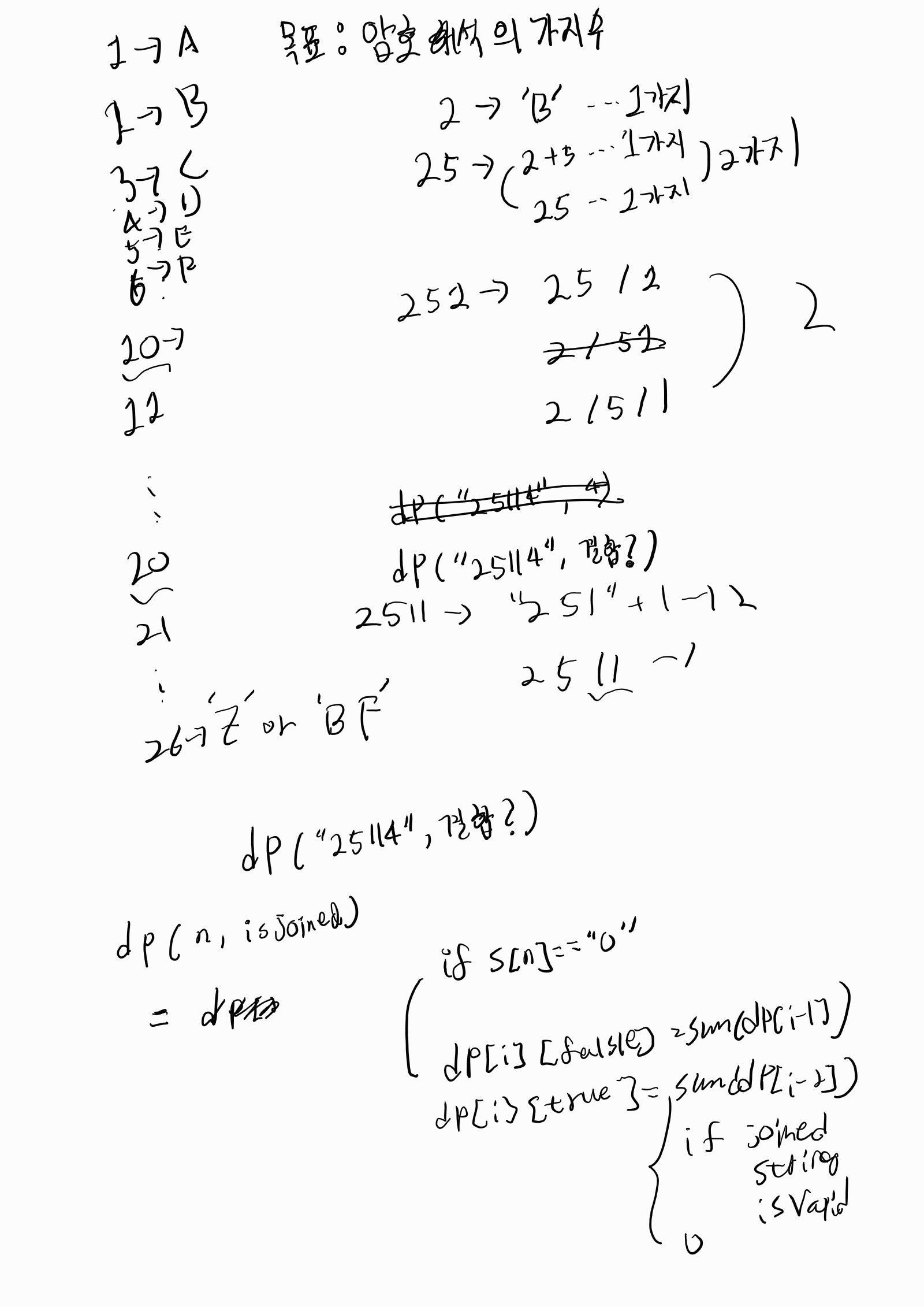
점화식의 핵심은 내가 현재 보고 있는 이 문자열이 따로 톡 떼놓았을 때 valid한가? 그리고 이전 문자열과 합쳤을 때 또 valid한가?였습니다.
왜냐면 암호코드는 1 ~26까지 범위에만 있으니깐요 ㅎㅎ

구현

import sys

input = sys.stdin.readline

if __name__ == "__main__":
    MOD = 1000_000
    S = input().strip()
    dp = [[0 for __ in range(2)] for _ in range(len(S))]
    dp[0][0] = 1 if S[0] != "0" else 0
    validJoinString = ["11","12","13","14","15","16","17","18","19","21","22","23","24","25","26"]
    for i in range(1, len(S)):
        if S[i] == "0":
            # 이전 문자와 결합하지 않는 경우
            dp[i][0] = 0
            # 이전 문자와 결합하는 경우
            dp[i][1] = dp[i - 1][0] % MOD if S[i - 1] == '1' or S[i - 1] == '2' else 0
        else:
            tmpStr = S[i - 1] + S[i]
            # print(tmpStr)
            dp[i][0] = dp[i - 1][0] % MOD + dp[i - 1][1] % MOD
            dp[i][0] %= MOD
            if i == 1:
                dp[i][1] = 1 if tmpStr in validJoinString else 0
            else:
                dp[i][1] = dp[i - 2][0] % MOD + dp[i - 2][1] % MOD if tmpStr in validJoinString else 0
                dp[i][1] %= MOD
    # print(dp)
    print((dp[len(S) - 1][0] % MOD + dp[len(S) - 1][1] % MOD)% MOD)

사실 지금 바텀업 점화식을 좀 더 명료하게 정리할 수 있지 않을까 싶은데요… 일단 AC를 받았으니 여기까지 하겠습니다.
그리고 맞왜틀이 있었는데요, 항상 모듈로 연산을 잘 해 줍시다.